多状态空间信息网络拓扑生成优化算法
随着“空天地一体化”进程的推进,空间信息网络(Space Information Network,SIN)在信息的传输、获取和分发任务中起着极其重要的作用。与地面网络不同,卫星网络中通信节点高速运动,通信链路频繁断开,信息传输的时延大、误码率高[1],严重影响网络拓扑的稳定性。而稳定的卫星网络拓扑不仅是实现网络信息交换和资源共享的基础,而且也是实现网络管理、协议设计优化、安全控制等的前提。因此,设计可靠的卫星网络拓扑算法至关重要。
卫星节点本身是一个多状态系统。多状态系统的定义及可靠性概念在20世纪70年代首次被提出[2-5],实际上,卫星在轨运行期间,由于零部件老化,负载及储能损耗等,卫星系统性能逐渐劣化,系统从正常工作到完全失效需要经历一系列中间过渡状态,这些不同状态导致了卫星实际上的工作性能不同,即卫星工作中具有多态性。
传统的卫星网络拓扑生成算法大多仅考虑卫星网络的空间特性,即看作分布在近地空间的一般节点,石磊玉等[6]针对如何有效分配有限波束来建立星间链路的问题,提出了一种基于贪婪算法的分配策略,在保证卫星观测数量最大化的前提下,以降低整网通信代价为优化目标,实现链路分配,但贪婪算法在该处的收敛性不佳。Chu和Chen[7]提出了一种基于北斗导航系统的时分拓扑生成算法,从拓扑角度实现源节点到端节点数据的快速传输。Ma等[8]提出一种新的低轨-中轨(Low Earth Orbit-Medium Earth Orbit, LEO-MEO)双层卫星网络拓扑模型,并考虑了极地边界的影响,但该模型工程上难以实现。Wang等[9]提出了一种综合权重的策略对卫星网络建链,减少了时延,拥塞率和链路切换。董明佶等[10]设计了一种改进的模拟退火算法,以空间位置精度因子(Position Dilution of Precision,PDOP)和网络时延等为优化目标,生成卫星激光星间链路拓扑,但是针对激光链路,与微波链路不同。
上述算法均未考虑卫星节点的多状态,仅考虑卫星节点位置等因素,当某节点状态不佳时,而不改变原有拓扑,将导致网络时延增大等问题。本文考虑卫星系统的多状态特点,利用现有的卫星星座,以连接度和可视距离等为约束条件,针对卫星网络高动态性,以链路平均端到端时延和最大端到端时延为优化目标,设计了一种改进的多目标模拟退火(Improved Multi-Objective Simulated Annealing,IMOSA)算法进行拓扑生成,使该算法在考虑卫星多状态的情况下,对卫星拓扑具有较好的优化效果,得到全局最优拓扑结构的近似解,并证明了生成的卫星网络拓扑的可靠性和抗毁性。
1 卫星系统的多状态随着卫星的长时间使用,将会有电阻、电容发生老化,磁盘机械磨损,故障率提升等现象,并且当卫星节点数据并发量过大,导致CPU和存储读写繁忙,都会导致处理能力下降,读取数据速度变慢等问题。本文依据卫星处理能力将其划分为不同的状态等级,卫星在每一刻的状态对应一个确定的状态等级,状态等级越低,误码率越高,处理能力越差,越容易出现故障,从而导致处理时延和排队时延增加,再加上由于星间距离产生的大传播时延,使得整体时延变大。
假设卫星状态等级集合为g={0, 1, …, m}。仿照实际情况,假设卫星性能水平服从一定的概率分布,状态最佳的卫星数量最多,一定比例出现状态较差的卫星。不同状态的卫星发送时延、处理时延和排队时延之和不同,当卫星处于状态R∈{0, 1, …, m}时,其发送时延、处理时延和排队时延之和t分别满足范围t∈{[ti, ti+1), [ti-1, ti),…, [ti-m, ti-m+1)},即存在映射关系。例如本文取0, 1, 2这3个状态:状态2,时延t∈[0, 20)最小;状态1,时延t∈[20, 100);状态0,t∈[100, ∞)最大,卫星状态最差。
2 卫星网络模型 2.1 卫星网络拓扑模型星间链路拓扑实际上是一个各边权值为星间距离的无向图[8-10]。描述为G (S, E),其中;S={s1, s2, …,sn}为n颗卫星的有限节点集,表示网络中卫星节点;E为有限边集,表示网络中卫星间的链路。通常用矩阵表示图,如建立n×n的矩阵A,当卫星si和卫星sj之间连通时,aij=1,否则aij=0,当i=j时aij=0,其中i, j=1, 2, …, n。称A为卫星网络的邻接矩阵,其表达式为
| $ \mathit{\boldsymbol{A}}=\left[ {\begin{array}{*{20}{c}} 0&{{a_{12}}}& \cdots &{{a_{1n}}}\\ {{a_{21}}}&0& \cdots &{{a_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{a_{n1}}}&{{a_{n2}}}& \cdots &0 \end{array}} \right] $ | (1) |
设矩阵V为卫星网络的可视矩阵,表示卫星由于地球的遮挡,呈现可视或不可视状态的矩阵。当卫星si和卫星sj之间可视时,vij=1,否则,vij=0。其表达形式与矩阵A类似。由于卫星在轨运行时相互会被地球遮挡,因而2颗卫星之间的链路长度存在一个满足可视条件的最大值。假设Hi、Hj分别表示卫星si、sj的轨道高度;Rd为地球半径,ξ为2颗卫星与地心形成的夹角。此时dmax为卫星si、sj可视的最大链路长度,即
| $ \begin{array}{*{20}{c}} {{d_{\max}}={{\left[ {{{\left( {{R_{\rm{d}}} + {H_i}} \right)}^2} - {{\left( {{R_{\rm{d}}}} \right)}^2}} \right]}^{\frac{1}{2}}} + }\\ {{{\left[ {{{\left( {{R_{\rm{d}}} + {H_j}} \right)}^2} - {{\left( {{R_{\rm{d}}}} \right)}^2}} \right]}^{\frac{1}{2}}}} \end{array} $ | (2) |
设dij为2颗卫星之间的实际距离,其计算公式为
| $ {d_{ij}}=\sqrt {{{\left( {{X_i} - {X_j}} \right)}^2} + {{\left( {{Y_i} - {Y_j}} \right)}^2} - {{\left( {{Z_i} - {Z_j}} \right)}^2}} $ | (3) |
式中:
| $ \begin{array}{l} {X_ * }=H\left[ {\cos m\cos \left( {\mathit{\Omega } - {\mathit{\Omega }_{\rm{G}}}} \right) - } \right.\\ \;\;\;\;\;\left. {\sin m\sin\left( {\mathit{\Omega } - {\mathit{\Omega }_{\rm{G}}}} \right)\cos\alpha } \right] \end{array} $ | (4) |
| $ \begin{array}{l} {Y_ * }=H\left[ {\cos m \sin\left( {\mathit{\Omega } - {\mathit{\Omega }_{\rm{G}}}} \right) - } \right.\\ \;\;\;\;\;\left. {\sin m\cos \left( {\mathit{\Omega } - {\mathit{\Omega }_{\rm{G}}}} \right)\cos\alpha } \right] \end{array} $ | (5) |
| $ {Z_ * }=H\left( {\sin m\sin \alpha } \right) $ | (6) |
| $ m={m_{\rm{a}}} + {n_0}\left( {t - {t_0}} \right) $ | (7) |
| $ {\mathit{\Omega }_{\rm{G}}}={\omega _{\rm{e}}}\left( {t - {t_0}} \right) $ | (8) |
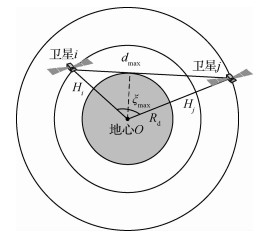
式中:*=i, j;ma为卫星真近地点角;n0为线速度;ωe为地球自转角速度;Ω为卫星升交点赤经,α为卫星轨道倾角,X、Y、Z分别为单颗卫星的地固坐标系。该坐标系的原点为地心,XOY平面和地球赤道平面重合,OX轴与格林威治子午线方向一致,OZ轴与地球的极轴重合。若不考虑其他天体和人造卫星对卫星的影响,由式(3)~式(7)得到星间距离dij。当dij≤dmax时,卫星可视,vij=1,否则为不可视,vij=0。可视性判断示意图如图 1所示。
|
| 图 1 卫星可视性判断示意图 Fig. 1 Judgment of satellites' visibility |
卫星在轨道上的相对运动使得互相之间的可视性随时间变化,为了减少这种由拓扑动态性引起的拓扑变化的复杂程度,本文将卫星星座周期长度T分成N个时间片[11-12]。这样时变的可视性卫星周期就转化为一系列拓扑固定的时间片,而在此基础上设计算法就能以每个时间片作为计算对象。
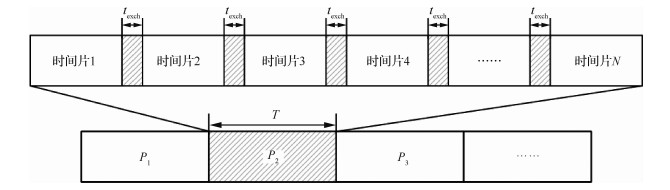
在每个时间片内,卫星拓扑不变,因此也称为拓扑快照。这种方法将周期T分成如下N个时间片:[t0=0, t1], [t1, t2], [t2, t3], …, [tN-1, tN=T],在新时间片开始处,存在链路交换时间texch,用来完成从上一个拓扑快照交换链路后生成下一个拓扑快照,时间片分割示意如图 2所示,其中Pi(i=1, 2, …, N)为周期。
|
| 图 2 时间片分割示意图 Fig. 2 Sketch map of time slots |
以上星座时间片的切换,由地面站配合完成。地面站分为主控站、监测站和注入站,主控站同时也是监测站[13]。监测站跟踪监控卫星状态,主控站依据已知星历和监测站反馈的信息运算各个时间片的拓扑和修正参数,转换为每颗卫星的建链信息发给注入站,注入站可见卫星由注入站直接上注,否则通过星间链路转发上注,进而完成时间片之间的链路交换。
3 卫星网络拓扑生成算法 3.1 算法建模卫星网络的拓扑生成算法实际上是寻找在满足卫星约束条件的前提下,生成的网络拓扑矩阵A的全局最优解。其中,卫星拓扑在每个时间片之间动态变化,算法需要在多条件约束下求出每个时间片的矩阵A的全部集合。仅对于有66颗卫星的铱星星座来说,矩阵A的取值空间就有265×32=22 080,若采取给优化目标赋予权值并遍历取值空间的做法,将是难以完成的任务。因此需要一种寻找矩阵A最优解的策略,使得算法能在有效时间内逼近全局最优解,故提出一种IMOSA算法以解决上述问题。
卫星拓扑生成可以转化为一个多目标优化的问题,本文依据卫星通信的实际情况,综合考虑卫星间链路约束条件,以网络平均时延、最大时延为优化目标,建立多目标优化的数学模型,对生成星间链路拓扑结构问题进行求解,多目标优化问题的数学模型可以表示为
| $ \min f\left( \mathit{\boldsymbol{A}} \right)={\left[ {{f_{{ au _a}}}\left( \mathit{\boldsymbol{A}} \right),{f_{{ au _m}}}\left( \mathit{\boldsymbol{A}} \right)} \right]^{\rm{T}}} $ | (9) |
式中:f为最优化的目标函数,试求解A=[aij](i, j=1, 2, …, n),A为链路拓扑矩阵的无向图模型,aij∈{0, 1}表示一个时间片中卫星si与卫星sj是否建立星间链路;τa、τm分别为星间链路的端到端时延的平均值和最大值,fτa(A)、fτm(A)是其二者关于A的优化函数。其计算公式为
| $ { au _{\rm{a}}}=\frac{1}{{n\left( {n - 1} \right)}}\sum\limits_{i=1}^n {\sum\limits_{j=1,j e i}^n {{c_{ij}}} } $ | (10) |
| $ { au _{\rm{m}}}=\max {c_{ij}} $ | (11) |
式中:cij(i, j=1, 2, …, n)表示在一个时间片内卫星si与sj之间链路的平均最小端到端时延。
建链约束条件为
| $ {\rm{s}}.\;{\rm{t}}.\;\;\;{v_{ij}} \in \left\{ {0,1} \right\} $ | (12) |
| $ {v_{ij}}={v_{ji}}\;\;\;\;\;\;\forall i,j $ | (13) |
| $ {v_{ij}} - {a_{ij}} \ge 0\;\;\;\;\;\;\forall i,j $ | (14) |
| $ \sum\limits_{j=1}^n {{a_{ij}}} \le k\;\;\;\;\;\forall i,j $ | (15) |
| $ {c_{ij}} < \infty \;\;\forall i,j $ | (16) |
式中:vij为星间链路可视矩阵,其值与卫星相对距离等有关;k为连接度。式(12)表示可视矩阵元素取值只能为1或0,即建链或断开;式(13)为矩阵的对称性约束;式(14)表示卫星拓扑至少满足可视性条件;式(15)表示卫星节点存在最大连接度k;式(16)表示任意2颗卫星之间通信时延不能是无限大,即卫星网络拓扑始终为连通图。
3.2 IMOSA算法多目标模拟退火(MOSA)算法是一种启发式算法,Kirkpatrick等将退火思想引入组合优化领域,提出了模拟退火算法[14]。该算法采用Metropolis接受准则,并用一组称为冷却进度表的参数控制算法进程,使算法求出问题的近似最优解。在每次迭代中接受较优解,并以一定的概率接受未优化解,从而获得跳出局部最优解的能力。
本文以前述多目标优化模型为MOSA算法模型,选取平均端到端时延、最大端到端时延作为优化目标,对传统MOSA算法进行改进,结合多状态特点,设计了符合卫星网络拓扑的邻域解生成IMOSA算法。IMOSA算法采用修改的Metropolis准则,相较于标准Metropolis准则更好地处理多目标的情况,并通过加入Pareto解集、和每隔一定迭代次数从Pareto解集中进行优选的策略,来保存历史最优值,以确保最终结果是最优解,相比一般MOSA算法,优化了迭代寻找最优解的方向,使之能更好地找到最优解,从而改善了收敛效果,提高了收敛速度。
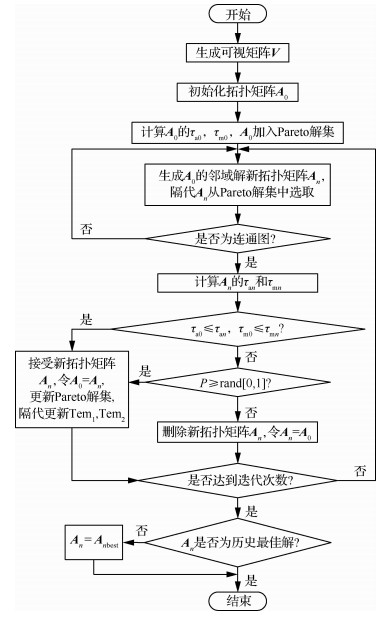
IMOSA算法流程如图 3所示。初始拓扑矩阵A0为待优化的静态拓扑矩阵,将其加入到Pareto解集中。每次迭代生成邻域解An,若新矩阵An的τa和τm均优于前一次,则令其为新的当前矩阵An,每隔一定迭代次数从Pareto解集中随机选择一个矩阵作为初始矩阵,重新搜索;如果新矩阵未被接受,则保留当前矩阵进行下一次迭代。接受概率为
|
| 图 3 IMOSA算法流程 Fig. 3 Process of IMOSA algorithm |
| $ P=\min \left\{ {1,\left[ {{\rm exp}\left( {\frac{{ - \Delta { au _{\rm{a}}}}}{{{\rm{Te}}{{\rm{m}}_1}}}} \right){\rm exp}\left( {\frac{{ - \varDelta { au _{\rm{m}}}}}{{{\rm{Te}}{{\rm{m}}_2}}}} \right)} \right]} \right\} $ | (17) |
式中:Δτa=τan-τa,Δτm=τmn-τm,表示新矩阵和原矩阵平均端到端时延和最大端到端时延的差值;Tem1、Tem2为IMOSA算法冷却进度表中的温度参数。冷却进度表是IMOSA算法效果的重要影响因素,其取值将影响最终优化结果。冷却进度表参数主要有:初始温度参数、温度更新参数、迭代终止条件。初始温度影响算法的优化效率,取值越大获得最优解概率越大,但迭代次数会增加,因此需折中取值。本文取平均端到端时延和最大端到端时延的方差分别为Tem1、Tem2的值。通过2个优化目标的乘积形式,使二者同时影响接受概率,协同优化。温度更新函数Temk+1=λBTemk,λB为Boltzmann常数,一般地0 < λB < 1,每隔一定代数降一次温。迭代终止条件为设定外循环次数来控制,历经多次迭代后逼近拓扑的全局最优解。IMOSA算法是通过搜索矩阵An的邻域解来找到最优解的,若直接随机交换,将会导致新的链路不满足可视条件或连接度条件,从而无法正确交换链路。
因此如何生成满足约束条件的邻域解,并且具有相当的随机性是重要问题。完成这一步骤,实际上是迭代中实现链路交换得到邻域解,需要找到交换后不影响约束条件的可交换的卫星。假设随机选取卫星s1和s2,找到其在拓扑矩阵A和可视矩阵V中对应行a1、v1和a2、v2,计算a3=a2 & a1 & v2,这里将矩阵行信息当作二进制进行位运算,即在已经与卫星s1建链的卫星序列中,找到尚未卫星与s2建链的卫星序列,但满足和卫星s2建链条件的卫星序列a3,同理计算a4=a1 & a2 & v1;再随机选择a3和a4中值为1的卫星号,记为卫星s3和s4,那么卫星s3和s4即是可以与s1和s2交换链路的卫星,则交换链路s1-s3和s2-s4至s1-s4和s2-s3,因为交换是对称的,所以卫星连接度未改变,且卫星是随机从a3和a4序列中选取的,因此该交换满足约束条件,并具有随机性。
在多状态条件下,卫星的状态值将影响卫星链路发送时延、处理时延和排队时延,加上星间动态的传播时延,即为端到端时延。运用Dijkstra算法进行求解卫星端到端时延,并依据卫星不同状态赋予链路权值,进而实现时延增大的效果。同时,若生成的图为不连通图,则必然至少出现某一端到端时延为无限大,那么算法将返回上一步骤重新交换链路,从而保证拓扑始终为连通图。因为拓扑矩阵具有对称性,只用计算上三角的时延即可,以减少Dijkstra算法的运算量。
3.3 算法复杂度在整个算法程序中,除了计算网络时延的最短路径算法Dijkstra算法外,其他模块均为O(N)或O(1)复杂度。在计算网络时延过程中,需要对每颗卫星求解一次最短路径,即执行N次Dijkstra算法。而算法中每一步找到最小值需要花费O(N)时间,从而整个算法过程花费O(N2)时间查找最小值;每次更新最短路径的时间为常数,而每条边最多更新一次,若有E条边则花费O(E)。因此总的复杂度为
| $ N\left[ {O\left( {{N^2}} \right) + O\left( E \right)} \right]=O\left( {{N^3}} \right) $ | (18) |
综上,IMOSA算法的复杂度为O(N3)。
4 仿真分析 4.1 仿真环境本文利用MATLAB和STK软件进行联合仿真,仿真采用具有66颗LEO的铱星星座(Iridium Constellation)作为星座构型。其具体参数如表 1所示。
| 卫星参数 | 数值 |
| 轨道高度/km | 780 |
| 轨道倾角/(°) | 86.3 |
| 轨道数目 | 6 |
| 轨道卫星数目 | 11 |
| 卫星总数 | 66 |
| 轨道面升交点赤经差/(°) | 60 |
| 轨道周期/s | 6 027.1 |
| 连接度 | 4 |
仿真中设卫星状态等级m=2,即有0,1,2这3个状态,因为实际卫星在轨运动期间,状态满足正态分布,大多数卫星状态都在2和1之间,状态为0的占少数,研究过程中发现,随着状态0和状态1的比例变大,算法优化效果变明显,但比例过大算法将失去优化空间。由于上述比例不符合正态分布的实际情况,因此本文不多加叙述。故假设状态分布概率参数如表 2所示,状态2和状态1分别涵盖了大约60%,35%的卫星,状态0的卫星仅占5%,符合实际情况。之后在卫星所属状态映射的区间内,随机产生卫星链路发送时延、处理时延和排队时延。星间传播时延由实时更新的星间距离与无线电在真空传播速度之比得到。
| 卫星状态 | 概率分布/% |
| 状态0 | 5 |
| 状态1 | 35 |
| 状态2 | 60 |
卫星坐标每1 s更新一次,可视矩阵改变即进入下一时间片,开始执行算法。IMOSA算法的冷却进度表中的初始温度参数T1、T2分别取均匀抽样的一组网络拓扑状态中的各自目标函数值的方差。其取值在不同时间片和星座中不同。另外温度更新函数设为λB=0.95较为合理[15-16],外循环迭代次数为2 000次。
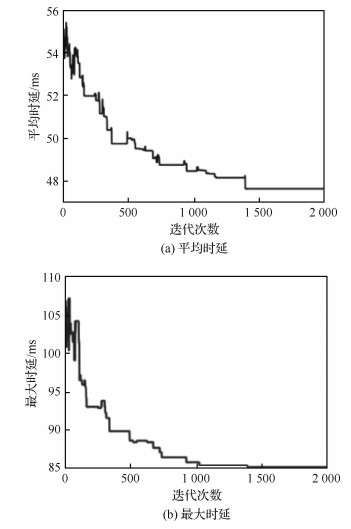
图 4为单个时间片内,IMOSA算法在铱星星座中,以平均时延和最大时延为目标,生成拓扑过程的收敛性能。由图 4可知,在迭代次数达到1 500次之前目标函数值已经收敛。相较于初始拓扑,两目标函数分别优化了11%和15%。另外从图中可以看出,随着迭代次数增加,目标函数值并非单调递减,而是会出现先增后再减小到更小值的情况,印证了IMOSA算法具有跳出局部最优解的性能。
|
| 图 4 单个时间片IMOSA算法收敛特性 Fig. 4 Convergence character of single time slot based on IMOSA |
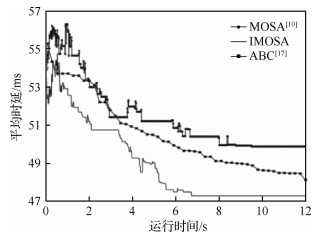
较新提出的启发式算法有蜂群(Artificial Bee Colony,ABC)算法[17-18]等,图 5为本文提出的IMOSA算法,与文献[10]中一般的MOSA算法、文献[17]中蜂群算法的收敛性进行对比。在保持其他条件一致的情况下,均对铱星星座进行拓扑生成仿真实验,统计在本文算法达到2 000次迭代的时间内各算法的收敛情况。如图 5所示,本文算法完成2 000次迭代的时间为12.03 s,在相同时间内,文献[10]的一般MOSA算法和文献[17]中的ABC算法收敛度均低于本文算法。实验表明,一般MOSA算法难以收敛到最优解,ABC算法虽然最终收敛效果好,但算法复杂度高,运行时间长。本文改进的MOSA算法兼顾收敛效果和运行时间,具有一定优越性。
|
| 图 5 IMOSA、MOSA和ABC算法收敛情况比较 Fig. 5 Comparison of convergence curves among IMOSA, MOSA and ABC algorithms |
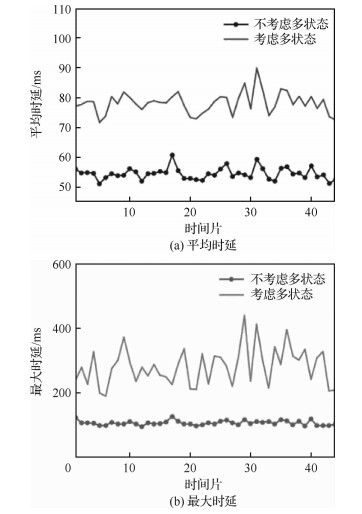
图 6为是否考虑多状态情况时,卫星网络时延的对比。由图可知在多状态情况下,端到端平均时延和最大时延均明显增大,且时延抖动也变大。因为事实上不考虑多状态的情况相当于假设所有卫星均处于最佳状态,当考虑多状态时,状态差的卫星影响了网络性能,而且在切换至下一个时间片时,状态差的卫星位置和与其他卫星链接状态发生改变,导致最大时延激增或锐减,同时平均时延也受到影响。
|
| 图 6 铱星星座中考虑多状态因素时的网络时延改变 Fig. 6 Variation of network time delays considering multi-states in Iridium Constellation |
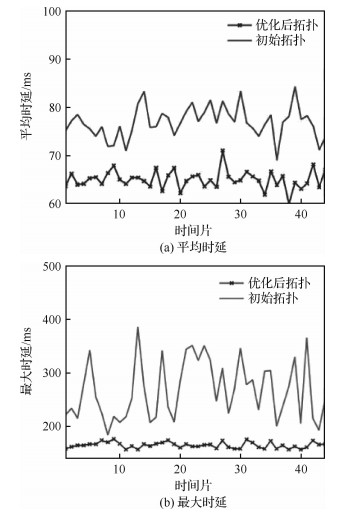
在均考虑卫星多状态的情况下,通过本文IMOSA算法生成的动态拓扑,其平均时延和最大时延相较于未优化的初始静态拓扑均有降低,原因是算法执行过程中,尽量避免了与状态差的卫星节点建链。如图 7(a)和图 7(b)所示,2个目标函数分别降低16%和34%,验证了算法的有效性。
|
| 图 7 铱星星座多状态下的IMOSA算法优化效果 Fig. 7 Results of optimization of IMOSA algorithm considering multi-states in Iridium Constellation |
本文对生成拓扑的抗毁性进行了分析。抗毁性刻画了网络被破坏的难易程度,由于节点间连接的抗毁性取决于节点之间替代途径的冗余性,那么网络的抗毁性就可以说取决于网络中替代途径的冗余性[19-20]。本文以自然连通度[21-22]作为网络拓扑的抗毁性指标,自然连通度刻画了网络中替代途径的冗余性。其计算公式为
| $ \bar \lambda=\ln \left( {\frac{1}{n}\sum\limits_{i=1}^n {{{\rm{e}}^{{\lambda _i}}}} } \right) $ | (19) |
式中:λi为拓扑邻接矩阵的特征根;n为拓扑节点个数。自然连通度关于拓扑抗毁性是严格单调的,拓扑结构抗毁性越强,自然连通度值越大。
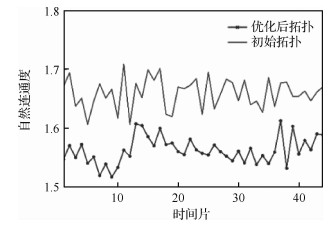
图 8为用IMOSA算法优化后的拓扑结构与原始拓扑结构自然连通度对比。如图所示,IMOSA算法优化后,在铱星星座中自然连通度λ的值都有所增大,由于卫星节点较少且连接度小,其增大并不明显(6%左右),但由于其严格的单调性已经表明拓扑结构的抗毁性提高。另外,图 9选择其中一个时间片,采用随机摧毁卫星节点的方式,显示了经优化后的拓扑在节点损毁时,自然连通度下降稍慢,即抗毁性更好。故证明了本文算法在一定程度上也保证了拓扑的抗毁性。
|
| 图 8 IMOSA算法优化前后自然联通度对比 Fig. 8 Comparison of natural connectivity of whether using IMOSA algorithm |

|
| 图 9 单个时间片随机删除节点后自然联通度对比 Fig. 9 Comparison of natural connectivity between deleting nodes in single time-slot |
本文针对空间信息网络多状态的情况,分析了多状态下卫星网络时延增大的问题,提出了一种以卫星网络平均时延和最大时延为目标函数的IMOSA算法,用以生成优化卫星星座拓扑,减小多状态下的网络时延。通过仿真验证:
1) 该算法在铱星星座中收敛性较MOSA算法和ABC算法更好,与静态拓扑相比,网络端到端平均时延和最大时延分别最大降低16%和34%,实现了网络拓扑的优化。
2) 同时自然连通度的值提高了6%,即该算法生成的网络拓扑具有更好的抗毁性。




