基于B-spline的轨迹优化
2024-06-10 05:52:35
常见的全局路径规划算法生成的路径通常有很多拐点,这对于机器人的运动是不利的,突然拐弯会浪费大量时间,对机器人控制也增加了复杂度。
本文基于B-splines对之前在ROS下的A*算法进行优化,生成更平滑的路径。
样条是分段多项式函数,广泛用于插值数据点或近似函数,曲线和曲面。B样条曲线是用于路径平滑的强大工具,可以针对不同的次数和障碍物配置生成所需的轨迹,广泛用于计算机图形学(Computer Graphics)、计算机辅助设计(Computer-Aided Design)等计算机领域。
1 B-spline曲线
1.1 基函数
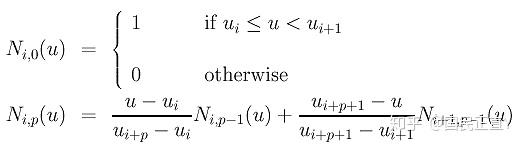
u为节点,p为次数;
1.2 B-spline
对于n+1个控制点 ,knot vectorU={u0,u1, ...,um},B曲线表示为:
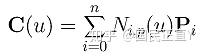
a set of n+1 control points, a knot vector of m+1 knots, and a degree p. Note that n,m and p must satisfy m=n+p+1.
如11个点(n=10),次数为3(p=3),则m=14.
在路径规划中用B样条时,要用clamped曲线,即第一个和最后一个点的knots=p+1.
2 Python实验
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import BSpline
def B(x, k, i, t):
if k == 0:
return 1.0 if t[i] <= x < t[i+1] else 0.0
if t[i+k] == t[i]:
c1 = 0.0
else:
c1 = (x - t[i])/(t[i+k] - t[i]) * B(x, k-1, i, t)
if t[i+k+1] == t[i+1]:
c2 = 0.0
else:
c2 = (t[i+k+1] - x)/(t[i+k+1] - t[i+1]) * B(x, k-1, i+1, t)
return c1 + c2
def bspline(x, t, c, k):
n = len(c)
return sum(c[i] * B(x, k, i, t) for i in range(n))
def main():
k = 3 #degree, k越大,曲线越逼近原始控制点
t = [] #knots vector
c1 = [-1.0, 1.0, 2.0, 2.5, 3.0, 3.0, 3.0, 3.0, 3.5, 5.0, 6.0, 8.0, 9.0] #x轴的路点
c2 = [0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 2.0, 3.0, 3.0, 3.0, 3.0, 3.5, 5.0] #y轴的路点
num = len(c1)
print "num:", num, "k:", k
for i in range(num+k+1):
if i <= k:
t.append(0)
elif i >= num:
t.append(num-k)
else:
t.append(i-k)
print "t:", t
spl_x = BSpline(t, c1, k)
spl_y = BSpline(t, c2, k)
plt.plot(c1, c2, '-og', label="Waypoints")
xx = np.linspace(0.0, num-k, 100)
plt.plot(spl_x(xx), spl_y(xx), '-r', label="B-Spline")
plt.grid(True)
plt.legend()
plt.axis("equal")
plt.show()
if __name__ == '__main__':
main()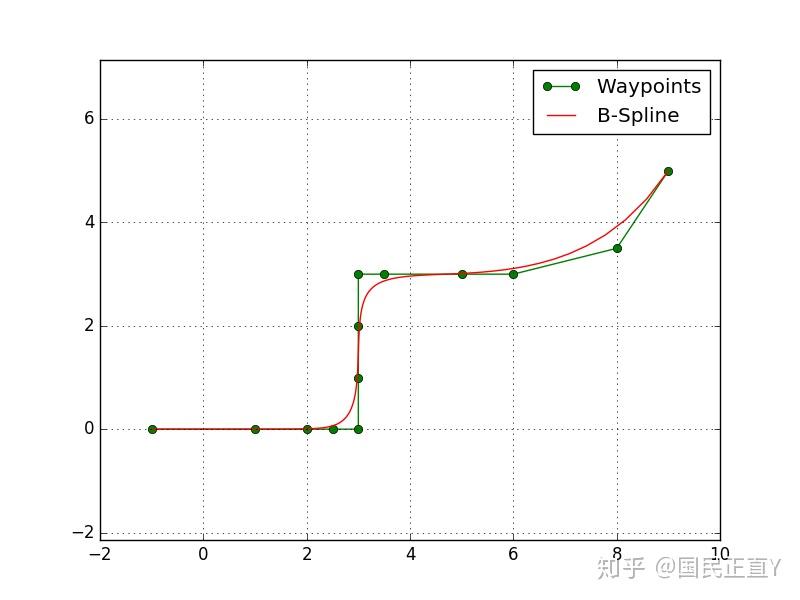
3 A* & B-spline in ROS
对A*生成的所有路径点进行B样条优化,在ROS仿真中出现move_base等待超时,初步判断是由于原始路径的点太多,导致轨迹优化插件超过了move_base的等待时间。
后来加了个迭代过程,对原始的所有点在一定间隔删除再进行B样条插值优化,生成的路径更加平滑。
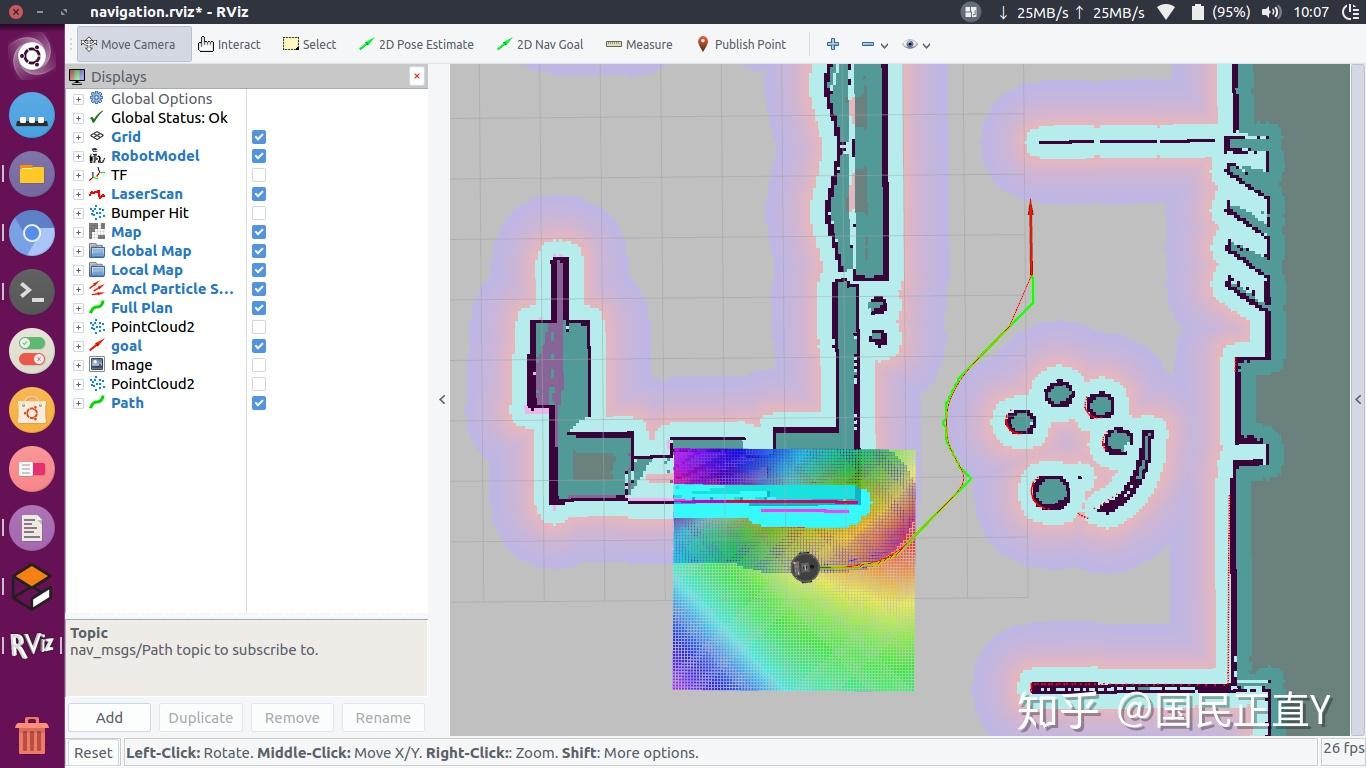
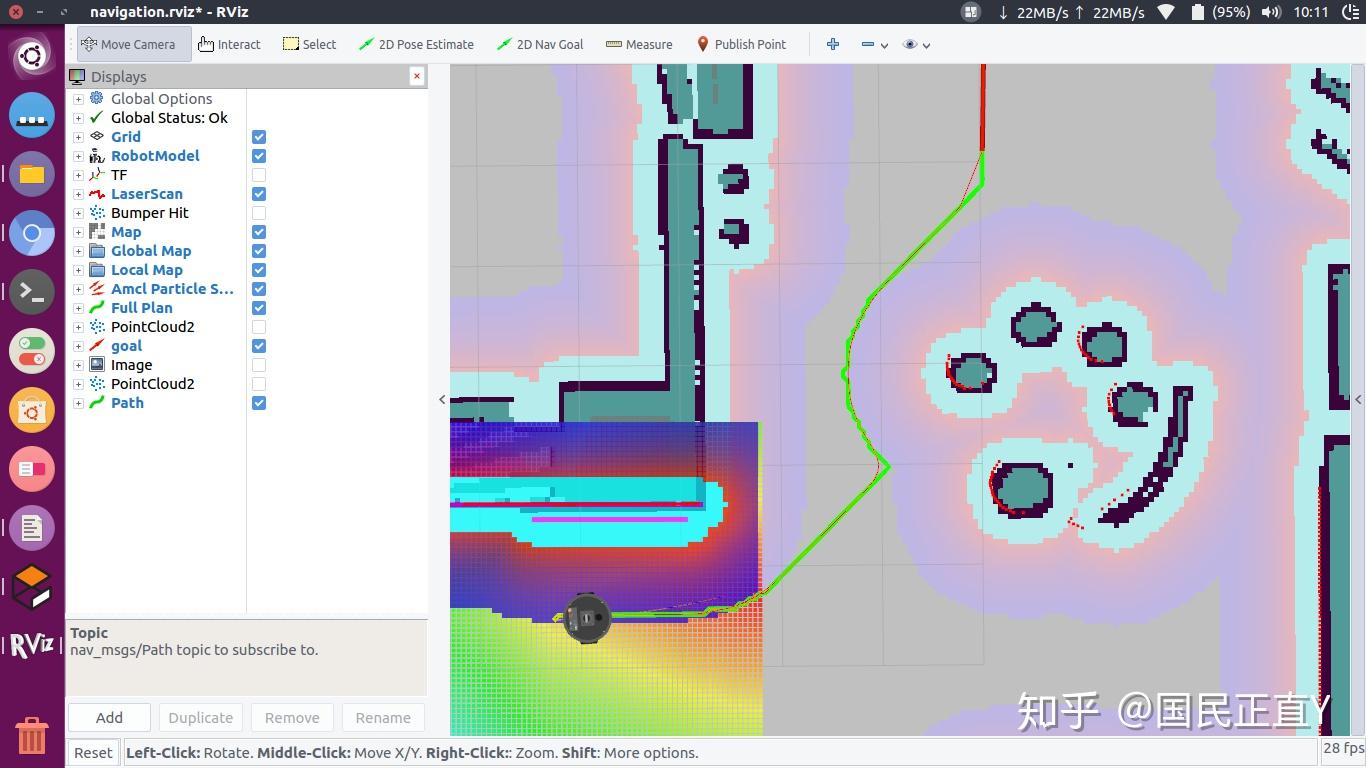
图中绿色粗线为原始路径,红色细线为优化后路径。
源码:
https://github.com/hubery05/A-start-with-B-spline



