Machine Learning学习笔记(十一)优化算法的总结
关于优化:我们每个人都会在我们的生活或者工作中遇到各种各样的最优化问题,比如每个企业和个人都要考虑的一个问题“在一定成本下,如何使利润最大化”等。最优化方法是一种数学方法,它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称。
我们现在学习的机器学习算法,大部分的机器学习算法的本质都是建立优化模型,通过最优化方法对目标函数(或损失函数)进行优化,从而训练出最好的模型。
传统:最优化算法 ————现代:启发式算法
常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、共轭梯度法等等。
1.1 梯度下降法
不加以赘述
1.2 牛顿法和拟牛顿法(Newton's method&Quasi Newton's method)
从本质上去看,牛顿法是二阶收敛,梯度下降是一阶收敛,所以牛顿法就更快。如果更通俗地说的话,比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。
 推广为向量的情况
推广为向量的情况
其中表达式中(下三角θ?(θ))表示的?(θ)对?θi的偏导数;H是一个n*n的矩阵,称为Hessian矩阵?。Hessian矩阵的表达式为: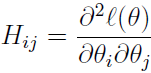
牛顿法的优缺点总结:
优点:二阶收敛,收敛速度快;
缺点:牛顿法是一种迭代算法,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
拟牛顿法(Quasi-Newton Methods)
拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使用正定矩阵来近似Hessian矩阵的逆,从而简化了运算的复杂度。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化,构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法,尤其对于困难的问题。另外,因为拟牛顿法不需要二阶导数的信息,所以有时比牛顿法更为有效。如今,优化软件中包含了大量的拟牛顿算法用来解决无约束,约束,和大规模的优化问题。
1.3?共轭梯度法
? 共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。?在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
?
?共轭梯度法不需要预先给定Q共轭方向,而是随着迭代的进行不断产生Q共轭方向。在每次的迭代中,利用上一个搜索方向和目标函数在当前迭代点的梯度向量 之间的线性组合构造一个新的方向,使其与前边已经产生的搜索方向组成Q共轭方向。对于一个n维二次型函数,沿着Q共轭方向进行搜索,经过n次迭代,即可得到极小点。?
共轭梯度法的算法步骤可以归纳如下:
?将“适者生存”进化规律模式化的优化搜索技术。
2.1.1?遗传算法(Genetic Algorithm,GA)
遗传算法是模拟生物在自然环境下的遗传和进化过程而形成的自适应随机全局搜索和优化方法。
算法操作过程:解决方案群中逐次产生一个近似最优解,称为一代;在每一代中,根据个体在问题域中的适应度和自然遗传学中借鉴来的再造方法进行选择,产生一个新的近似解,即下一代。新个体比原个体更适应环境。
优点是能很好的处理约束,能很好的跳出局部最优,最终得到全局最优解,全局搜索能力强;缺点是收敛较慢,局部搜索能力较弱,运行时间长,且容易受参数的影响。遗传算法适合求解离散问题,具备数学理论支持,但是存在着汉明悬崖等问题。
2.2.2 差分进化算法(Differential Evolution,DE)
? ? 差分进化算法是基于群体智能理论的优化方法,是通过群体内个体间的合作与竞争产生的智能优化搜索。
? ? 与进化算法相同之处:使用全局搜索策略
? ? 与进化算法不同之处:基于差分的简单编译操作;“一对一”的竞争生存策略;具有记忆能力,可跟踪搜索情况以调整搜索策略。
? ? 免疫算法是模仿生物满意机制,采用群体搜索策略并迭代计算;利用自身多样性和维持机制,克服“早熟”问题,求解全局最优。
? ? 群智能算法是一种基于生物群体行为规律的计算技术,用来解决分布式问题。这种犯法只需要目标函数的输出值,不需要其梯度信息。
? ? 蚁群算法是通过模拟自然界中蚂蚁集体寻径行为而提出的一种基于种群启发式随机搜索算法。
? ? 方法:蚂蚁在走过的路径上留下信息素;后来的蚂蚁大概率选择信息素强的路径;信息素强度大会吸引更多蚂蚁,形成正反馈,最终找到最短路径。
? ? 特点:分布式计算、无中心控制、分布式个体间间接通信等特征。
适合在图上搜索路径问题,计算开销会大。
2.2.2 粒子群算法(Particle Swarm Optimization,PSO)
? ? 粒子群算法是一种基于群体智能的全局随机搜索算法。
? ? 与其他进化算法相同之处:基于“种群”、“进化”概念,进行个体竞争
? ? 与其他进化算法不同之处:不进行交叉、变异、选择等进化算子操作;而是将个体向吱声历史最佳位置和领域历史最佳位置集聚。
? ? 应用:非线性、多峰问题。
适合求解实数问题,算法简单,计算方便,求解速度快,但是存在着陷入局部最优等问题。
2.3?模拟退火算法(Simulated Annealing,SA)
? ? 模拟退火算法是一种基于迭代求解策略的随机寻优算法;局部搜索算法的扩展,以一定的概率选择领域只能怪目标值最大的状态。
? ? 特点:克服局部极值的缺陷和对初值的依赖性。
? ? 方法:定义邻域结构;在邻域结构内选取相邻解;利用目标函数进行评估。
优点是局部搜索能力强,运行时间较短;缺点是全局搜索能力差,容易受参数的影响。
2.4 ?禁忌搜索算法(Tabu Search or Taboo Search,TS)
? ? 通过禁忌准则来避免重复搜索;通过藐视准则来赦免一些被禁忌的优良状态。
2.5 神经网络算法(Artificial Neural Network,ANN)
? ? 神经网络是一种模仿生物神经系统 新的信息处理模型。







